User-agent: Mediapartners-Google
Disallow:
For model questions and previous years questions visit http://www.en2k6questions.blogspot.com
Wednesday, May 7, 2008
Monday, February 18, 2008
INTERFERENCE OF LIGHT
Everyone is familiar with the beautiful colours produced by a thin film of oil on the surface of water and also by the thin film of a soap bubble. These beautiful colour effects arise from interference between light waves
(1)Reflected and
(2)Transmitted from the two surfaces of thin transparent films.
Interference due to reflected light
Consider a transparent film of thickness‘t’ and refractive index ‘µ’. A ray AB is incident on the upper surface of the film. The light partly gets reflected along BP and partly refracted along BC. At C, part of it is reflected along CD and finally emerges out along DQ. The rays BP and DQ interfere and we observe interference pattern.
(1)Reflected and
(2)Transmitted from the two surfaces of thin transparent films.
Interference due to reflected light
Consider a transparent film of thickness‘t’ and refractive index ‘µ’. A ray AB is incident on the upper surface of the film. The light partly gets reflected along BP and partly refracted along BC. At C, part of it is reflected along CD and finally emerges out along DQ. The rays BP and DQ interfere and we observe interference pattern.
The path difference between the two rays BP and DQ can be calculated. Draw DM normal to BP and CN normal to BD. It is evident from figure,
Ð BCN = r and Ð BDM = i
Optical path difference between the two waves = µ (BC+CD) - BM
But from figure, BC = CD
\ Optical path difference = 2µBC-BM ----- (1)
From D BCN, cos r = CN/BC = t/BC
Or BC = t/cos r ----- (2)
From D BDM, sin i = BM/BD
Or BM = BD sin i ----- (3)
From D BCN, tan r = BN/CN = BN/t
Or BN = t tan r
But BD = 2 BN
\ BD = 2 t tan r ----- (4)
Substituting the value of BD from equation (4) in equation (3),
BM = 2 t tan r sin i
=2 t sin r/cos r x sin i
=2 t sin r/cos r x sin i/sin r x sinr
=2 µ t sin2r/cos r ----- (5) [µ = sin i/sin r]
Substituting the value of BM from equation (5) and BC from equation (2) in equation (1),
Optical path difference = 2 µ t/cos r - 2 µ t/cos r x sin2r
= 2 µ t/cos r [1 - sin2r]
= 2 µ t/cos r x cos2r
= 2 µ t cos r
By electromagnetic theory, when light is reflected from the surface of an optically denser medium, a phase change ofp, equivalent to a path difference of l/2 occurs.
\ Correct path difference = 2 µ t cos r - l/2
Condition for constructive interference ( Bright bands)
Path difference = nl
\ 2 µ t cos r - l/2 = nl
2 µ t cos r = nl + l/2
2 µ t cos r = (n+1) l/2
Condition for destructive interference (Dark bands)
Path difference = (2n+1) l/2
\ 2 µ t cos r - l/2 = (2n+1) l/2
2 µ t cos r = (2n+1) l/2 + l/2
= (2n+2) l/2
= (n+1) l
Since n is an integer, (n+1) can also be taken as n.
\ 2 µ t cos r = nl
Colours in thin films
When light is incident on a thin film, the reflected light will not include the colour whose wavelength satisfies the equation 2 µ t cos r = nl. Therefore the film will appear coloured and the colour will depend upon thickness and the angle of incidence (refraction). If ‘r’ and‘t’ are constant, the colour will be uniform. In the case of oil on water, different colours are observed because ‘r’ and‘t’ vary.
Ð BCN = r and Ð BDM = i
Optical path difference between the two waves = µ (BC+CD) - BM
But from figure, BC = CD
\ Optical path difference = 2µBC-BM ----- (1)
From D BCN, cos r = CN/BC = t/BC
Or BC = t/cos r ----- (2)
From D BDM, sin i = BM/BD
Or BM = BD sin i ----- (3)
From D BCN, tan r = BN/CN = BN/t
Or BN = t tan r
But BD = 2 BN
\ BD = 2 t tan r ----- (4)
Substituting the value of BD from equation (4) in equation (3),
BM = 2 t tan r sin i
=2 t sin r/cos r x sin i
=2 t sin r/cos r x sin i/sin r x sinr
=2 µ t sin2r/cos r ----- (5) [µ = sin i/sin r]
Substituting the value of BM from equation (5) and BC from equation (2) in equation (1),
Optical path difference = 2 µ t/cos r - 2 µ t/cos r x sin2r
= 2 µ t/cos r [1 - sin2r]
= 2 µ t/cos r x cos2r
= 2 µ t cos r
By electromagnetic theory, when light is reflected from the surface of an optically denser medium, a phase change ofp, equivalent to a path difference of l/2 occurs.
\ Correct path difference = 2 µ t cos r - l/2
Condition for constructive interference ( Bright bands)
Path difference = nl
\ 2 µ t cos r - l/2 = nl
2 µ t cos r = nl + l/2
2 µ t cos r = (n+1) l/2
Condition for destructive interference (Dark bands)
Path difference = (2n+1) l/2
\ 2 µ t cos r - l/2 = (2n+1) l/2
2 µ t cos r = (2n+1) l/2 + l/2
= (2n+2) l/2
= (n+1) l
Since n is an integer, (n+1) can also be taken as n.
\ 2 µ t cos r = nl
Colours in thin films
When light is incident on a thin film, the reflected light will not include the colour whose wavelength satisfies the equation 2 µ t cos r = nl. Therefore the film will appear coloured and the colour will depend upon thickness and the angle of incidence (refraction). If ‘r’ and‘t’ are constant, the colour will be uniform. In the case of oil on water, different colours are observed because ‘r’ and‘t’ vary.
NEWTON’S RINGS-REFLECTED SYSTEM
When a plano convex lens is placed on a glass plate, a thin film of air is enclosed between the lower surface of the lens and upper surface of the plate. The thickness of the film is very small at the point of contact and gradually increases from the centre outwards. Concentric circular fringes are produced, uniform in thickness with the point of contact as the centre. When viewed with white light, the fringes are colored. With monochromatic light, bright and dark circular fringes are produced.
Here interference is due to the light reflected from the lower surface of the lens and upper surface of the glass plate. The fringes are circular because the air film has a circular symmetry.
Theory
Suppose the radius of curvature of the lens is R. The thickness of the air film be‘t’ at a distance ‘r’ from the centre.
From figure,
AB2 + BC2 = AC2
i.e. (R-t)2 + r2 = R2
R2 + t2- 2Rt + r2 = R2
2Rt = t2 + r2
Since t is very small, t2 can be neglected.
\ 2Rt = r2
Or, t = r2/2R ----- (1)
Dark rings
Condition is 2 µ t cos r = nl
For air film, µ = 1. For normal incidence, cos r = 1
\2t = nl
Substituting‘t’ from equation (1),
2r2/2R = nl
r2 = nlR
rn = ÖnlR
Diameter of nth dark ring, Dn = 2rn = Ö4nlR
Bright rings
Condition is 2 µ t cos r = (2n+1)l/2
For air film, µ = 1. For normal incidence, cos r = 1
\2t = (2n+1)l/2
Substituting‘t’ from equation (1),
2r2/2R = (2n+1)l/2
r2 = (2n+1)lR/2
rn = Ö(2n+1)lR/2
Diameter of nth bright ring, Dn = 2rn = Ö2(2n+1)lR
Determination of wavelength of light using Newton’s rings experiment
With the help of traveling microscope, measure the diameters of mth and nth dark rings.
Dm = Ö4mlR
Dn = Ö4nlR
Dm2 - Dn2 = 4(m-n) lR
\l = Dm2 - Dn2 / 4(m-n)R
Here interference is due to the light reflected from the lower surface of the lens and upper surface of the glass plate. The fringes are circular because the air film has a circular symmetry.
Theory
Suppose the radius of curvature of the lens is R. The thickness of the air film be‘t’ at a distance ‘r’ from the centre.
From figure,
AB2 + BC2 = AC2
i.e. (R-t)2 + r2 = R2
R2 + t2- 2Rt + r2 = R2
2Rt = t2 + r2
Since t is very small, t2 can be neglected.
\ 2Rt = r2
Or, t = r2/2R ----- (1)
Dark rings
Condition is 2 µ t cos r = nl
For air film, µ = 1. For normal incidence, cos r = 1
\2t = nl
Substituting‘t’ from equation (1),
2r2/2R = nl
r2 = nlR
rn = ÖnlR
Diameter of nth dark ring, Dn = 2rn = Ö4nlR
Bright rings
Condition is 2 µ t cos r = (2n+1)l/2
For air film, µ = 1. For normal incidence, cos r = 1
\2t = (2n+1)l/2
Substituting‘t’ from equation (1),
2r2/2R = (2n+1)l/2
r2 = (2n+1)lR/2
rn = Ö(2n+1)lR/2
Diameter of nth bright ring, Dn = 2rn = Ö2(2n+1)lR
Determination of wavelength of light using Newton’s rings experiment
With the help of traveling microscope, measure the diameters of mth and nth dark rings.
Dm = Ö4mlR
Dn = Ö4nlR
Dm2 - Dn2 = 4(m-n) lR
\l = Dm2 - Dn2 / 4(m-n)R
AIR WEDGE/WEDGE SHAPED THIN FILM
Let an air wedge be formed between two glass plates, slightly inclined to each other at an angle q as shown. Illuminate the wedge by a parallel beam of monochromatic light. Interference occurs between the rays reflected from the upper and lower surfaces of the air film. Alternate dark and bright bands of equal width are observed.
Let‘t’ be the thickness of the air film at a distance ‘x’ from the edge. From figure,tanq = t/x
Since q is small, tanq~q
\q = t/x
Or t = qx ----- (1)
Condition for occurrence of a dark band is
2 µ t cos r = nl
For air film, µ = 1. For normal incidence, cos r = 1
\2t = nl
Substituting‘t’ from equation (1),
2qx = nl
Or, xn = nl/2q
\ xn+1 = (n+1)l/2q
Fringe width b = xn+1 - xn
= l/2q
For a liquid wedge,
b = l/2µq
Applications of air wedge
Determination of thickness (diameter) of thin objects
The given object is placed between two glass plates to form an air wedge. On illumination, we can see alternate bright and dark bands with bandwidth b = l/2q
Determination of thickness (diameter) of thin objects
The given object is placed between two glass plates to form an air wedge. On illumination, we can see alternate bright and dark bands with bandwidth b = l/2q
From figure,q = d/L
\ b = lL/2d
Or, d = lL/2b
Testing of optical planeness of surfaces
A surface is said to be optically flat if it is plane upto 1/10 th of the wavelength of light used. In order to test the planeness, we can use interference fringes obtained from an air film. The surface to be tested is placed in contact with an optically flat glass plate and the fringes are viewed. If the fringes of equal thickness are formed, then the surface is flat. Irregular and distorted fringe pattern is obtained if the surface is not flat.
DIFFRACTION OF LIGHT
Diffraction of light
When a narrow slit AB is placed in the path of light, then only part A’B’ of the screen should be illuminated and no light should enter the geometrical shadow regions A’X and B’Y of the screen. On the other hand, when obstacle AB is placed, then its distinct geometrical shadow is A’B’.
It happens exactly so only when the size of the slit or obstacle is large. However, if the size of the obstacle is made small, of the order of wavelength of light used, then light enters into the geometrically prohibited regions showing thereby that light bends round the corners of the slit or obstacle.
This phenomenon of bending of light round the corners and spreading of light into the regions of geometrical shadow is called diffraction.
Fresnel and Fraunhoffer diffraction
Based on the relative positions of the source and screen with respect to the object causing diffraction, we have two classes of diffraction-Fresnel and Fraunhoffer.
In fresnel diffraction, either the source of light or the screen or both are at finite distances from the obstacle causing diffraction. Here to get the diffraction effect on the screen, no modification is made by lenses and mirrors.
Example: Diffraction at a single slit
In Fraunhoffer diffraction, both the source and screen are at infinite distances from the object causing diffraction. In actual practice, the source and the screen are placed at the focal planes of two convex lenses. Then both the source and image(screen) are effectively at infinity.
Diffraction Grating
An arrangement which is equivalent in action to a number of parallel,euidistant,narrow rectangular slits of equal width placed side by side is called diffraction grating.
Gratings are made by ruling equidistant parallel lines on an optically transparent sheet of material, the line portion being opaque and the space between the lines being transparent to light. This sheet acts as a transmission grating. To get a reflection grating, lines are drawn on a plane silvered surface.
In the construction of good quality grating, the following considerations must be taken into account.
(1) It should have large number of slits (the number of lines should be large).
(2) The spacing between the lines should be equal.
Original gratings are quite expensive. Hence their photographic reproductions or replicas are used.
Theory
Let XY represent a plane transmission grating. AB represent an opaque portion and BC a slit. Let ‘a’ be the width of each slit and ‘b’ the width of an opaque portion. The distance (a+b) is called the grating element.
Let a parallel beam of monochromatic light of wavelength l be incident normally on the grating surface. Most of the light go go straight, but a part of it gets diffracted. When focused by a convex lens L, maximum intensity is observed at P, the focus of the convex lens.
Since the width of the slit is of the order of wavelength of light, part of the light get diffracted at the slit, in different directions. Consider the secondary waves originating from A and C proceeding at an angle q with the normal. The path difference between the waves on reaching the point O is,
AN = (a+b) sinq
Condition for maximum intensity, (a+b) sinq = nl
If there are N lines/meter in a grating, a+b = 1/N
\sinq = nNl ----- (1)
This is known as grating equation.
Intensity distribution of diffraction pattern
P corresponds to the position of central maximum and 1, 2 etc. on the two sided of P represent the 1st, 2nd etc. principal maxima. a,b,c etc. are secondary maxima and d,e etc. are secondary minima.
When a narrow slit AB is placed in the path of light, then only part A’B’ of the screen should be illuminated and no light should enter the geometrical shadow regions A’X and B’Y of the screen. On the other hand, when obstacle AB is placed, then its distinct geometrical shadow is A’B’.
It happens exactly so only when the size of the slit or obstacle is large. However, if the size of the obstacle is made small, of the order of wavelength of light used, then light enters into the geometrically prohibited regions showing thereby that light bends round the corners of the slit or obstacle.
This phenomenon of bending of light round the corners and spreading of light into the regions of geometrical shadow is called diffraction.
Fresnel and Fraunhoffer diffraction
Based on the relative positions of the source and screen with respect to the object causing diffraction, we have two classes of diffraction-Fresnel and Fraunhoffer.
In fresnel diffraction, either the source of light or the screen or both are at finite distances from the obstacle causing diffraction. Here to get the diffraction effect on the screen, no modification is made by lenses and mirrors.
Example: Diffraction at a single slit
In Fraunhoffer diffraction, both the source and screen are at infinite distances from the object causing diffraction. In actual practice, the source and the screen are placed at the focal planes of two convex lenses. Then both the source and image(screen) are effectively at infinity.
Diffraction Grating
An arrangement which is equivalent in action to a number of parallel,euidistant,narrow rectangular slits of equal width placed side by side is called diffraction grating.
Gratings are made by ruling equidistant parallel lines on an optically transparent sheet of material, the line portion being opaque and the space between the lines being transparent to light. This sheet acts as a transmission grating. To get a reflection grating, lines are drawn on a plane silvered surface.
In the construction of good quality grating, the following considerations must be taken into account.
(1) It should have large number of slits (the number of lines should be large).
(2) The spacing between the lines should be equal.
Original gratings are quite expensive. Hence their photographic reproductions or replicas are used.
Theory
Let XY represent a plane transmission grating. AB represent an opaque portion and BC a slit. Let ‘a’ be the width of each slit and ‘b’ the width of an opaque portion. The distance (a+b) is called the grating element.
Let a parallel beam of monochromatic light of wavelength l be incident normally on the grating surface. Most of the light go go straight, but a part of it gets diffracted. When focused by a convex lens L, maximum intensity is observed at P, the focus of the convex lens.
Since the width of the slit is of the order of wavelength of light, part of the light get diffracted at the slit, in different directions. Consider the secondary waves originating from A and C proceeding at an angle q with the normal. The path difference between the waves on reaching the point O is,
AN = (a+b) sinq
Condition for maximum intensity, (a+b) sinq = nl
If there are N lines/meter in a grating, a+b = 1/N
\sinq = nNl ----- (1)
This is known as grating equation.
Intensity distribution of diffraction pattern
P corresponds to the position of central maximum and 1, 2 etc. on the two sided of P represent the 1st, 2nd etc. principal maxima. a,b,c etc. are secondary maxima and d,e etc. are secondary minima.
POLARISATION OF LIGHT
Polarisation
The experiments on interference and diffraction have shown that light is a form of wave motion. But these effects, do not give an idea about the type of wave motion. The phenomenon of polarization has helped to establish that light waves are transverse in nature.
Production of plane polarized light
Some of the methods for the production of plane polarized light are
The experiments on interference and diffraction have shown that light is a form of wave motion. But these effects, do not give an idea about the type of wave motion. The phenomenon of polarization has helped to establish that light waves are transverse in nature.
Production of plane polarized light
Some of the methods for the production of plane polarized light are
(1) Reflection,
(2) Refraction,
(3) Double refraction,
(4) Selective absorption in crystals and
(5) Scattering.
Polarisation by reflection
An ordinary beam of light on reflection from a transparent medium like glass, water etc. becomes partially polarized. The degree of polarization increases as the angle of incidence increased. At a particular value of angle of incidence, the reflected beam becomes completely polarized. This angle of incidence is called the polarizing angle (ip) for that medium.
Brewster’s law
Refractive index of the material medium is equal to tangent of the angle of polarization. This is called Brewster’s law.
i.e, µ = tan ip = sin ip/cosip ----- (1)
From Snell’s law, µ = sin ip/sin rp ----- (2)
Comparing (1) and (2), sin rp = cosip = sin (90- ip)
\rp = 90 – ip
Or, ip+rp = 900
i.e., when light is incident at the polarizing angle, the reflected and refracted rays are perpendicular to each other.
Double refraction (Birefringence)
It is seen that when a beam of ordinary monochromatic light is allowed to pass through a calcite or quartz crystal, we get two refracted beams instead of the usual one as in the case of glass. This phenomenon is called double refraction or birefringence.
When an illuminated pin hole is observed through a calcite crystal, two images are seen. If the crystal is rotated about the incident ray as axis, it is found that one of the images remains stationary while the other rotates round the stationary image. The stationary image is known as ordinary image while the other is known as extra ordinary image. The ray giving rise to the ordinary image is called the ordinary ray and the ray giving rise to the extra ordinary image is called extra ordinary ray.
The ordinary ray obeys laws of refraction while the extra ordinary ray does not. The refractive index of a doubly refracting crystal is a constant with respect to the ordinary ray. The refractive index of the crystal with respect to the extraordinary ray varies with the angle of incidence.
It has been found that both ordinary and extra ordinary rays are plane polarized with their vibrations being at right angles to each other. Ordinary ray has vibration perpendicular to the principal section and extra ordinary ray has vibration parallel to the principal section.
For a calcite crystal, rE is greater than ro. Therefore, µo is greater than µE.
Polarisation by reflection
An ordinary beam of light on reflection from a transparent medium like glass, water etc. becomes partially polarized. The degree of polarization increases as the angle of incidence increased. At a particular value of angle of incidence, the reflected beam becomes completely polarized. This angle of incidence is called the polarizing angle (ip) for that medium.
Brewster’s law
Refractive index of the material medium is equal to tangent of the angle of polarization. This is called Brewster’s law.
i.e, µ = tan ip = sin ip/cosip ----- (1)
From Snell’s law, µ = sin ip/sin rp ----- (2)
Comparing (1) and (2), sin rp = cosip = sin (90- ip)
\rp = 90 – ip
Or, ip+rp = 900
i.e., when light is incident at the polarizing angle, the reflected and refracted rays are perpendicular to each other.
Double refraction (Birefringence)
It is seen that when a beam of ordinary monochromatic light is allowed to pass through a calcite or quartz crystal, we get two refracted beams instead of the usual one as in the case of glass. This phenomenon is called double refraction or birefringence.
When an illuminated pin hole is observed through a calcite crystal, two images are seen. If the crystal is rotated about the incident ray as axis, it is found that one of the images remains stationary while the other rotates round the stationary image. The stationary image is known as ordinary image while the other is known as extra ordinary image. The ray giving rise to the ordinary image is called the ordinary ray and the ray giving rise to the extra ordinary image is called extra ordinary ray.
The ordinary ray obeys laws of refraction while the extra ordinary ray does not. The refractive index of a doubly refracting crystal is a constant with respect to the ordinary ray. The refractive index of the crystal with respect to the extraordinary ray varies with the angle of incidence.
It has been found that both ordinary and extra ordinary rays are plane polarized with their vibrations being at right angles to each other. Ordinary ray has vibration perpendicular to the principal section and extra ordinary ray has vibration parallel to the principal section.
For a calcite crystal, rE is greater than ro. Therefore, µo is greater than µE.
µE=1.486
µo=1.658
For a quartz crystal, rOis greater than rE. Therefore, µE is greater than µO.
µE=1.553
µo=1.544
Calcite crystal
Calcite crystals are generally used in polarisation experiments.It is transparent to visible and ultraviolet light.Chemically it is CaCO3 and assumes rhomohedron crystal structure
QUANTUM MECHANICS
Matter waves
The waves associated with a material particle are called matter waves. Wavelength of matter wave associated with a particle of momentum p is given by,
l=h/p --------- (1)
l is called de-Broglie wavelength.
Newtonian mechanics and quantum mechanics
In Newtonian mechanics or classical mechanics, the future state of a particle is completely determined by its initial position and momentum together with the forces that act upon it. In contrast to the above, the structure of quantum mechanics is built upon the foundation of particles which are purely probabilistic in nature. Thus instead of asserting, for example, the radius of electron orbit in a ground state of hydrogen atom is always exactly 0.53Å, quantum mechanics states that this is the most probable radius.
Quantum mechanics is related to microscopic universe while Newtonian mechanics deals with macroscopic universe.
Newton’s second law of motion is the basis of Newtonian mechanics while Schrödinger equation is the basis of quantum mechanics.
Heisenberg’s uncertainty principle
According to classical mechanics, it is possible for a particle to occupy a fixed position and have a definite momentum and we can predict exactly its position and momentum at any time later. But according to uncertainty principle, it is not possible to determine accurately the simultaneous values of position and momentum of a particle at any time. Heisenberg’s principle implies that in physical measurements, probability takes the place of exactness and as such phenomena which are impossible according to classical ideas may find a small but finite probability of occurrence.
Statement
It is impossible to determine precisely and simultaneously the values of both the members of a pair of physical variables which describe the motion of an atomic system. Such pairs of variables are called canonically conjugate variables.
Examples:1) Position and momentum
2) Energy and time
The waves associated with a material particle are called matter waves. Wavelength of matter wave associated with a particle of momentum p is given by,
l=h/p --------- (1)
l is called de-Broglie wavelength.
Newtonian mechanics and quantum mechanics
In Newtonian mechanics or classical mechanics, the future state of a particle is completely determined by its initial position and momentum together with the forces that act upon it. In contrast to the above, the structure of quantum mechanics is built upon the foundation of particles which are purely probabilistic in nature. Thus instead of asserting, for example, the radius of electron orbit in a ground state of hydrogen atom is always exactly 0.53Å, quantum mechanics states that this is the most probable radius.
Quantum mechanics is related to microscopic universe while Newtonian mechanics deals with macroscopic universe.
Newton’s second law of motion is the basis of Newtonian mechanics while Schrödinger equation is the basis of quantum mechanics.
Heisenberg’s uncertainty principle
According to classical mechanics, it is possible for a particle to occupy a fixed position and have a definite momentum and we can predict exactly its position and momentum at any time later. But according to uncertainty principle, it is not possible to determine accurately the simultaneous values of position and momentum of a particle at any time. Heisenberg’s principle implies that in physical measurements, probability takes the place of exactness and as such phenomena which are impossible according to classical ideas may find a small but finite probability of occurrence.
Statement
It is impossible to determine precisely and simultaneously the values of both the members of a pair of physical variables which describe the motion of an atomic system. Such pairs of variables are called canonically conjugate variables.
Examples:1) Position and momentum
2) Energy and time
Wavefunction
The quantity with which quantum mechanics is concerned is the wavefunction y of a particle. We can obtain all the physical properties of a system if we know the wavefunction. The quantity y2 or y*ydxdydz is proportional to the probability of finding the particle in the volume element dxdydz about the point (x,y,z).
If òy*ydxdydz=0, the particle does not exist.
If òy*ydxdydz=a, the particle is everywhere simultaneously
Since the particle exist somewhere at all times,
òy*ydxdydz=1 --------- (2)
The wavefunction y satisfying the above condition is called normalized wavefunction.
Requirements of wavefunction
The wavefunction must be continuous and single valued everywhere.
∂y/∂x, ∂y/∂y and ∂y/∂z must also be continuous and single valued everywhere.
y can be normalized.
Wave equation
A wave whose variable quantity is y that propagates in the x-direction with speed v is expressed by an equation,
∂2y/∂x2=1/v2 ∂2y/∂t2 --------- (3)
This is called wave equation.
Schrödinger’s equation for a free particle-time dependent equation
Schrödinger’s equation is a wave equation with the variabley. It is the fundamental equation of quantum mechanics in the same sense that the second law of motion is the fundamental equation of Newtonian mechanics.
The quantity with which quantum mechanics is concerned is the wavefunction y of a particle. We can obtain all the physical properties of a system if we know the wavefunction. The quantity y2 or y*ydxdydz is proportional to the probability of finding the particle in the volume element dxdydz about the point (x,y,z).
If òy*ydxdydz=0, the particle does not exist.
If òy*ydxdydz=a, the particle is everywhere simultaneously
Since the particle exist somewhere at all times,
òy*ydxdydz=1 --------- (2)
The wavefunction y satisfying the above condition is called normalized wavefunction.
Requirements of wavefunction
The wavefunction must be continuous and single valued everywhere.
∂y/∂x, ∂y/∂y and ∂y/∂z must also be continuous and single valued everywhere.
y can be normalized.
Wave equation
A wave whose variable quantity is y that propagates in the x-direction with speed v is expressed by an equation,
∂2y/∂x2=1/v2 ∂2y/∂t2 --------- (3)
This is called wave equation.
Schrödinger’s equation for a free particle-time dependent equation
Schrödinger’s equation is a wave equation with the variabley. It is the fundamental equation of quantum mechanics in the same sense that the second law of motion is the fundamental equation of Newtonian mechanics.
Eigen values and Eigen functions
By solving the Schrödinger equation, we obtain the possible set of y functions. In case of bound particles, the acceptable solutions for the differential equations are possible only for certain specified values of energy. These descrete values of energy E1,E2,........,En are called energy eigen values of the particle. The solutions y1,y2,...........,y3 corresponding to the eigen values are called eigenfunctions.
NMR AND ESR
NUCLEAR MAGNETIC RESONANCE(NMR)
Spin magnetic moment of proton is given by
µp= +/- 2.793 µN where µN=eh/4pMp is the nuclear magneton.
Spin magnetic moment of nuetron is given by
µn=-/+1.913µN
Spin magnetic moment of proton is given by
µp= +/- 2.793 µN where µN=eh/4pMp is the nuclear magneton.
Spin magnetic moment of nuetron is given by
µn=-/+1.913µN
At first glance, it seems odd that the neutron, with no net charge, has a spin magnetic moment. But if we assume that the neutrons contain equal amounts of positive and negative charges, a spin magnetic moment could arise even with no net charge.
Let E0 be the energy of the nucleus. When the nucleus is in a constant magnetic field B, magnetic moment of protons interacts with magnetic field B and the energy of interaction is given by µpB. As a result, the energy level E0 splits into two components E0+µpB and E0-µpB.
At this stage, magnetic moment vector M of the nucleus makes precession around the magnetic field direction. This precision is called Larmour precision. Larmour frequency for protons,
nL=ΔE/h=2µpB/h
Let E0 be the energy of the nucleus. When the nucleus is in a constant magnetic field B, magnetic moment of protons interacts with magnetic field B and the energy of interaction is given by µpB. As a result, the energy level E0 splits into two components E0+µpB and E0-µpB.
At this stage, magnetic moment vector M of the nucleus makes precession around the magnetic field direction. This precision is called Larmour precision. Larmour frequency for protons,
nL=ΔE/h=2µpB/h
If an electromagnetic radiation of frequency nL is now incident on the sample, the nuclei will receive the energy to flip their spins and reach the higher state. This phenomenon is called nuclear magnetic resonance (NMR). Radio frequency range electromagnetic radiations are used here.Experimental method for the detection of NMR
The specimen material is taken in a glass vessel and placed between the pole pieces of the magnet. The magnetic field acting between the pole pieces can be varied by changing the current through the sweep coil. Radio frequency generator supplies Radio frequency electromagnetic radiations to the specimen through Radio frequency coil wound round the specimen. At the same time Radio frequency generator supplies the signal to the external circuit which measures the power absorbed by the specimen. At resonance, the specimen absorbs energy from electromagnetic radiation and hence there occurs a drop in its amplitude. The absorption signal is amplified by the amplifier and finally displayed on a CRO.Applications of NMR
To study the molecular structure.
In chemical structure analysis of materials.
In the study of chemical reactions.
To study the internal and local electric fields in an alloy.
In the study of diffusion co-efficient.
For measuring nuclear magnetic moment.
For measuring magnetic field.
Electron spin resonance
Spin magnetic moment of electrons is measured in Bohr magneton. Bohr magneton is given by, µB=eh/4pme.
Let E0 be the energy of the electron. When such an electron is placed in a uniform magnetic field of strength B, the energy level E0 splits into two components E0+1/2gµBB and E0-1/2gµBB, where ‘g’ is called Lande’s factor. g=1 for pure orbital motion. g=2 for pure spin motion.
At this stage, magnetic moment vector M of the electron makes precession around the magnetic field direction B. This precision is called Larmour precision. Larmour frequency for protons,
nL=ΔE/h=gµBB/h
If an electromagnetic radiation of frequency nL is now incident on the sample, the electrons will receive the energy to flip their spins and reach the higher state. This phenomenon is called electron spin resonance (ESR). This occurs in elements having unpaired electrons.ESR exhibited by paramagnetic substances is called electron paramagnetic resonance (EPR). ESR exhibited by ferromagnetic substances is called ferromagnetic resonance (FMR).
Experimental method for the detection of ESR
A strong magnet with pole pieces M1 and M2 provides uniform magnetic field B. The low frequency modulator controls the magnetic field. A very high frequency generator supplies the energy at the time of resonance. Since high frequency oscillations are used, specimen is taken in a waveguide. At resonance, the radio frequency signal is noted and detected in detector. It is suitably amplified in an amplifier and finally recorded in a recorder.
Applications of ESRIn the study of organic, inorganic and biological systems.
To identify paramagnetic reaction intermediate in chemical reactions.
To locate the paramagnetic species in polymers, catalysts etc.
To determine the electronic structure of free radicals.
LASER
LASER IS THE SHORT FORM OF LIGHT AMPLIFICATION BY STIMULATED EMISSION OF RADIATION.
CHARACTERISTICS OF A LASER BEAM
1.DIRECTIONALITY:
LASER BEAM IS HIGHLY DIRECTIONAL.IT CAN BE FOCUSSED TO A FINE POINT.HENCE LASER IS USED FOR SURGICAL APPLICATIONS.
2.MONOCHROMATICITY:
LASER BEAM IS HIGHLY MONOCHROMATIC.LINE WIDTH IS NARROW COMPARING WITH CONVENTIONAL LIGHT SOURCES.FOR RUBY LASER LINE WIDTH = 5 ANGSTROM.
3.COHERENCE:
LASER BEAM IS HIGHLY COHERENT.TWO INDEPENDENT LASER SOURCES CAN PRODUCE INTERFERENCE EFFECTS.
4.BRIGHTNESS:
LASER IS HIGHLY INTENSE BEAM OF LIGHT.IT IS USED IN INDUSTRY FOR CUTTING,WELDING AND DRILLING OPERATIONS.
Basic concepts of laser
CHARACTERISTICS OF A LASER BEAM
1.DIRECTIONALITY:
LASER BEAM IS HIGHLY DIRECTIONAL.IT CAN BE FOCUSSED TO A FINE POINT.HENCE LASER IS USED FOR SURGICAL APPLICATIONS.
2.MONOCHROMATICITY:
LASER BEAM IS HIGHLY MONOCHROMATIC.LINE WIDTH IS NARROW COMPARING WITH CONVENTIONAL LIGHT SOURCES.FOR RUBY LASER LINE WIDTH = 5 ANGSTROM.
3.COHERENCE:
LASER BEAM IS HIGHLY COHERENT.TWO INDEPENDENT LASER SOURCES CAN PRODUCE INTERFERENCE EFFECTS.
4.BRIGHTNESS:
LASER IS HIGHLY INTENSE BEAM OF LIGHT.IT IS USED IN INDUSTRY FOR CUTTING,WELDING AND DRILLING OPERATIONS.
Basic concepts of laser
Interaction of radiation with matter
Consider a system having two energy levels E1 and E2 with E2-E1=hÖ. When it is exposed to radiation having a stream of photons, each with energy hÖ, three district processes can take place. They are 1) Absorption
2) Spontaneous emission and
3) Stimulated emission.Absorption
An atom in the ground state E1 can absorb a portion of energy hÖ and go to the higher energy state E2. This process is known as absorption and is illustrated in figure.Rate of absorption R12 is proportional to population (number of available atoms per unit volume) of the lower energy level N1 and u(Ö), the energy density of radiation u(Ö).i.e, R12 a N1u(Ö)R12 = B12N1u(Ö) ------------(1)
Where B12 is called Einstein coefficient.
Spontaneous EmissionIn spontaneous emission, the atoms in the higher energy state E2 eventually return to the ground state by emitting their excess energy spontaneously. This process is independent of the external radiation. The rate of spontaneous emission R21 is directly proportional to the population of the energy level E2 (N2).i.e, R21 a N2R21 = A21N2 --------------(2)
Spontaneous EmissionIn spontaneous emission, the atoms in the higher energy state E2 eventually return to the ground state by emitting their excess energy spontaneously. This process is independent of the external radiation. The rate of spontaneous emission R21 is directly proportional to the population of the energy level E2 (N2).i.e, R21 a N2R21 = A21N2 --------------(2)
Where A21 is called Einstein coefficient.Stimulated emissionIn stimulated emission, a photon having energy hÖ(E2-E1) stimulate an atom in the higher state E2 to make a transition to the lower state E1 with the creation of a second photon. The rate of stimulated emission R121 is proportional to population at the energy level E2(N2) and energy density of radiation u(Ö).i.e, R121 a N2u(Ö)
Semiconductor laser (Diode laser/GaAs laser)
GaAs is a direct bandgap semiconductor. Laser transition is possible only in direct bandgap semiconductors. Si and Ge do not give laser transition since they are indirect bandgap semiconductors.
Fermilevel (EF) is the highest filled energy level at absolute zero. A semiconductor in which Fermi level lies the conduction band (in n type) or valence band (in p type) is called a degenerate semiconductor. A p-n junction is used for the fabrication of semiconductor laser. Both p and n regions are made degenerate by heavy doping.
With a forward bias, depletion region (active region) contains a high concentration of electrons in the conduction band and holes in the valence band. Population inversion has occurred in the sense that more states are occupied in the conduction band than in the valence band. At low bias currents, electron-hole recombination takes place spontaneously resulting in a spontaneous emission of photons. This is the principle of a light emitting diode (LED). As the diode current increases, a point is reached, where significant population inversion exist near the junction resulting in a stimulated emission.
GaAs is a direct bandgap semiconductor. Laser transition is possible only in direct bandgap semiconductors. Si and Ge do not give laser transition since they are indirect bandgap semiconductors.
Fermilevel (EF) is the highest filled energy level at absolute zero. A semiconductor in which Fermi level lies the conduction band (in n type) or valence band (in p type) is called a degenerate semiconductor. A p-n junction is used for the fabrication of semiconductor laser. Both p and n regions are made degenerate by heavy doping.
With a forward bias, depletion region (active region) contains a high concentration of electrons in the conduction band and holes in the valence band. Population inversion has occurred in the sense that more states are occupied in the conduction band than in the valence band. At low bias currents, electron-hole recombination takes place spontaneously resulting in a spontaneous emission of photons. This is the principle of a light emitting diode (LED). As the diode current increases, a point is reached, where significant population inversion exist near the junction resulting in a stimulated emission.
One pair of faces perpendicular to the junction is polished so that they act as resonant cavity. The remaining faces are roughened to eliminate laser action in those directions. 
In a semiconductor laser, the transitions are associated with the electron states in the conduction band and valence band. The upper and lower energy states are continuous and hence the output is not sharp. Thus coherence and monochromaticity of a GaAs laser are poor. But they have a few advantages. They are*Portable since compact and small.
*High efficiency
*Highly economical
*Can produce both continuous wave and pulsed laser.
*Tuning of output is easily possible.
Applications of laser
1. Industrial application: Welding, drilling and cutting.
2. Medical applications: In dermatology, dentistry, ophthalmology, in surgery of tumours, kidney stone and for cancer treatment.
3. For making sensors.
4. In holography.
5. In laser printers.
6. In research.
7. In microelectronics.
8. In accelerating certain chemical reactions.
9. In fibre optic communication.
10. In underwater communication.
11. In military applications.
HOLOGRAPHY
The method of producing the 3-diamensional image of an object due to the interference phenomena of coherent light waves on a photographic plate is known as holography. The idea of holography was first developed by Dennis Gabber in 1948. The invention of laser during 1960 enhanced research in this field.
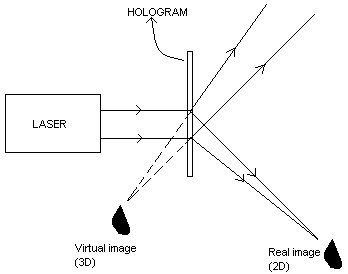
When an object is photographed by a camera, a 2-dimensional image of 3-dimensional object is obtained. Here only the amplitude of the light wave is recorded on the photographic film. In holography, both the phase and the amplitude of the light waves are recorded in the film. The resulting photograph is called hologram. In Greek, ‘holo’ means whole and ‘graphy’ means writing. So holography stands for whole writing. The recorded hologram has no resemblance to the original object. It has in it a coded form of information of the object. The image is reproduced by a process called reconstruction.
Recording of a hologram
The experimental arrangement for the recording of a hologram using a laser beam is shown below:
When an object is photographed by a camera, a 2-dimensional image of 3-dimensional object is obtained. Here only the amplitude of the light wave is recorded on the photographic film. In holography, both the phase and the amplitude of the light waves are recorded in the film. The resulting photograph is called hologram. In Greek, ‘holo’ means whole and ‘graphy’ means writing. So holography stands for whole writing. The recorded hologram has no resemblance to the original object. It has in it a coded form of information of the object. The image is reproduced by a process called reconstruction.
Recording of a hologram
The experimental arrangement for the recording of a hologram using a laser beam is shown below:
A laser beam from a source is made to fall on an optical device called beam splitter. A part of the beam splitter is made to fall on a mirror M1. The beam is reflected waves from the mirror and made to fall on the object. The reflected waves from the surface of the object, called object wave, is made to fall on the photographic plate. The other part of the beam is made to fall on a mirror M2 and then to photographic plate. This beam is called reference wave. The object wave and reference wave interfere and the interference pattern characteristic of the object is recorded on the photographic plate. This recorded interference pattern gives hologram.Reconstruction of images
In order to view the image, hologram is to be illuminated with the laser having the same wavelength used for recording of the hologram. Illumination of the hologram results in two images - a two dimensional real image and a three dimensional virtual image.
Applications of holography1) In information storage in computers.
2) In fog droplet camera.
3) In dynamic aerosol camera.
4) In holographic interferometry.
5) In holographic cinema.
6) In acoustic holography.
7) In data processing.
8) Hologram can be used as an optical grating.
FIBRE OPTICS
Conventional methods of long distance communication use radio waves (~ 106 Hz) and micro waves (~1010 Hz) as carrier waves. A light beam acting as carrier waves is capable of carrying far more information since optical frequencies are extremely large (~1015 Hz).
Soon after the discovery of laser, some preliminary experiments in propogation of information carrying light waves through the open atmosphere wave carried out, but it was realized that the unwanted elements such as rain, fog etc. leads to adverse effects. Thus in order to have an efficient and dependable communication system one would require a guiding medium in which the information carrying light waves could be transmitted. This resulted in the development of optical fibre which is an efficient guiding medium for laser light.
Basic principle-total internal reflection
The basic principle of optical fibre is multiple total internal reflection. When a ray of light travel from denser to a rarer medium, at an angle of incidence greater than critical angle qc, the ray is not reflected but it is reflected into the same denser medium. This property is called total internal reflection. Light signals are transmitted through optic fibres by multiple total internal reflection.
Soon after the discovery of laser, some preliminary experiments in propogation of information carrying light waves through the open atmosphere wave carried out, but it was realized that the unwanted elements such as rain, fog etc. leads to adverse effects. Thus in order to have an efficient and dependable communication system one would require a guiding medium in which the information carrying light waves could be transmitted. This resulted in the development of optical fibre which is an efficient guiding medium for laser light.
Basic principle-total internal reflection
The basic principle of optical fibre is multiple total internal reflection. When a ray of light travel from denser to a rarer medium, at an angle of incidence greater than critical angle qc, the ray is not reflected but it is reflected into the same denser medium. This property is called total internal reflection. Light signals are transmitted through optic fibres by multiple total internal reflection.
Fibre construction and fibre dimensionAn optical fibre consists of a vary thin transparent cylindrical core having refractive index n1 surrounded by a cylindrical shell called cladding of slightly lower refractive index n2. The core cladding system is surrounded by plastic jackets.
Optical fibres are hair thin threads of glass or plastic. Plastic fibres have the advantage of more flexibility than glass fibres but attenuation is greater in plastic fibres, comparing with glass fibres.
Core diameter ranges from 5 to 600µm. Cladding diameter ranges from 125 to 750µm. The thickness of the jacket is around 100µm. totally optical fibre has an outer diameter ranging from 0.1mm to 1.5 mm.
Light propogation in optical fibres
Consider an optical fibre with n1 and n2 as the refractive indices of core and cladding material respectively. Consider a ray of light entering through one end making an angle q with the axis.
By Snell’s law, n1=sini/ sinqOr sinq=sini/ n1 ------(1)
At core –cladding interface, refractive index µ=n1/n2
Total internal reflection takes place at core-cladding interface if the angle of incidence at core-cladding interface is equal or greater than critical angleÆc.
We have µ=n1/n2=1/sinÆc
sinÆc=n2/n1 -----(2)
For total internal reflection to take place,
Æ > Æc
or, sinÆ > sinÆc
i.e, sinÆ > n2/n2 (from equ(2))
But from figure, sinÆ =cosq
cosq > n2/n1
i.e, (1-sin2q)1/2 > n2/n1
1-sin2q > (n2/n1)2
sin2q < sinq =" sini/n1">Acceptance angle
The maximum angle of incidence at which light may enter the fibre in order to be propagated is, im= sin-1(n2-n22)1/2
This angle is called acceptance angle for the fibre.
Numerical aperture
Numerical aperture of an optical fibre is a measure of its gathering capacity and it is denoted as the sine of acceptance angle.
i.e, NA=sinim=(n2-n22)1/2
Step index and graded index fibre
If the optical fibre has a core of uniform constant refractive index n1 and a cladding of slightly lower refractive index n2, it is called a step index fibre. The cross sectional refractive index profile is as shown:
If the core of optic fibre has a non-uniform refractive index that decreases gradually from the centre towards the core-cladding boundary, it is called a graded index fibre. The cladding surrounding the core has a uniform refractive index, slightly lower than the refractive index of the core. The cross sectional refractive index profile is as shown:
Single mode and multimode fibreIn single mode fibres, only one mode of light rays are guided through the fibre. For this, a step index fibre with a small core diameter is used.
In multimode fibres, a number of modes of light rays guided through the fibres. For this, a step index fibre with a large core diameter or a graded index fibre is used.
Signal distortion and transmission losses
1) Attenuation
Absorption and scattering of light traveling through a fibre leads to decrease the strength of the signal which is referred as attenuation of the signal.
2) Intermodal dispersion
The intermodal dispersion occurs in multimode fibres where rays associate with various modes travel different distances through the fibre. As a result, the signal broadens and the output signal is no longer identical with the input signal. Signal broadening is less in graded index and step index single mode fibres.
3) Material dispersion or chromatic dispersion
If we use white light, all the colours of the input radiation are not reacting the other end at the same time since they travel with different velocities. This type of signal distortion is called material dispersion or chromatic dispersion.
4) Waveguide dispersion
In single mode fibres, 80% of signal travels through the core. The remaining 20% travels through the cladding, move faster than the signal through the core. The signal distortion occurring due to this is called waveguide dispersion. Waveguide dispersion is small in multimode fibres and can be ignored.
Light wave communication using optic fibre
A simple block diagram of fibre optic communication system is shown below:
Optical transmitterA light emitting diode (LED) or a semiconductor laser can be used as optical source. Modulation modulates the input signal and optical signal and then transmitted through optical fibre cables to the receiver.
Optical receiver
A photodiode can be used as optical detector. The detected wave is demodulated to extract the signal.
Advantage of fibre optic communication
1) Wide band width.
2) Low attenuation and other transmission losses.
3) Small size and weight.
4) Safe from electrical interference caused by lightning, electric motors, fluorescent tube and other electrical noise sources.
5) Lack of cross talk between parallel fibres.
6) Easy installation and easy maintenance.
7) Flexible.
8) Temperature resistance.
9) Highly economical.
10) High degree of signal security.
11) Longer life span.
Fibre amplifier
Fibre loss in optical fibres is the main disadvantage of fibre optic communication system. To overcome this, optical amplifiers are used. There are 4 types of optical amplifiers:
Erbium doped fibre amplifier (EDFA)
Fibre Raman amplifier (FRA)
Semiconductor laser amplifier (SLA) and
Integrated optical amplifier (IOA)
Erbium doped fibre amplifier (EDFA)
Here Erbium doped silica fibres are used. When incident photon energy is incident on a doped fibre, Erbium ions in the medium are made to move to higher energy levels. The Erbium ions in the excited state return to the ground state either spontaneously or by stimulation. Erbium doped fibres have long metastable states leading to coherent amplification. A practical configuration of EDFA is as shown:
Fibre loss in optical fibres is the main disadvantage of fibre optic communication system. To overcome this, optical amplifiers are used. There are 4 types of optical amplifiers:
Erbium doped fibre amplifier (EDFA)
Fibre Raman amplifier (FRA)
Semiconductor laser amplifier (SLA) and
Integrated optical amplifier (IOA)
Erbium doped fibre amplifier (EDFA)
Here Erbium doped silica fibres are used. When incident photon energy is incident on a doped fibre, Erbium ions in the medium are made to move to higher energy levels. The Erbium ions in the excited state return to the ground state either spontaneously or by stimulation. Erbium doped fibres have long metastable states leading to coherent amplification. A practical configuration of EDFA is as shown:
Advantages of EDFAHigh gain
High output power
Low noise
Less gain variation
Wide bandwidth
Compatible to transmission fibre with minimum loss
Cross talk immunity and
Low power consumption.
NON DESTRUCTIVE TESTING
User-agent: Mediapartners-Google* Disallow:
X-rays
In 1895, Roentgen found that a highly penetrating radiation of unknown nature is produced when fast moving electrons strikes on matter. Because of their unknown nature, Roentgen called these radiations as X-rays. Actually X-rays are electromagnetic waves of very short wavelength.
Properties of X-rays
1. They are electromagnetic waves of very short wavelength.
2. They travel in straight line with the velocity of light.
3. They can affect a photographic film.
4. They cause fluorescence in many materials.
5. They can ionize the gas through which they pass.
6. They can penetrate through matter.
7. They can cause photoelectric effect.
8. They are not deflected by electric and magnetic fields.
9. Under suitable conditions, X-rays are reflected and refracted like ordinary light.
Production of X-rays
A Coolidge tube (discharge tube) is used for the production of X-rays. The cathode is a tungsten filament F heated by a 5-10 V battery. By thermionic emission, electrons are emitted from the cathode. These electrons are accelerated to high velocities by applying a very high potential difference between the cathode and the anode. When accelerated electrons strike the target (anode), X-rays are produced.
In 1895, Roentgen found that a highly penetrating radiation of unknown nature is produced when fast moving electrons strikes on matter. Because of their unknown nature, Roentgen called these radiations as X-rays. Actually X-rays are electromagnetic waves of very short wavelength.
Properties of X-rays
1. They are electromagnetic waves of very short wavelength.
2. They travel in straight line with the velocity of light.
3. They can affect a photographic film.
4. They cause fluorescence in many materials.
5. They can ionize the gas through which they pass.
6. They can penetrate through matter.
7. They can cause photoelectric effect.
8. They are not deflected by electric and magnetic fields.
9. Under suitable conditions, X-rays are reflected and refracted like ordinary light.
Production of X-rays
A Coolidge tube (discharge tube) is used for the production of X-rays. The cathode is a tungsten filament F heated by a 5-10 V battery. By thermionic emission, electrons are emitted from the cathode. These electrons are accelerated to high velocities by applying a very high potential difference between the cathode and the anode. When accelerated electrons strike the target (anode), X-rays are produced.
X-ray radiography
Radiography means producing an image on a film using electromagnetic radiation. X-ray radiographic methods are used for non destructive testing. Cracks, voids, discontinuities in welded joints etc. can be detected by this method. X-ray radiography operates on the principle of dissimilar transmission of X-rays through different materials. The ability of the material to block X-rays increases with the density of the material.X-rays can penetrate easily through soft body tissues and are largely blocked by bone structure of other solid materials. So if a photographic plate is placed behind the patient, a photo can be taken showing bones as white shadows.
There are 3 main disadvantages:
X-ray image is basically a shadow and there is no scope for 3-dimensional informations.
X-rays are not easy to focus; hence images are of low resolution.
It is difficult to distinguish between various types of tissues in the body because they all have similar X-ray absorption properties.
To overcome these problems, stereo radiography and computed tomography (CT) are used.
Stereo radiography
Stereo radiography consists of superimposing radiographs taken from two positions of the X-ray tube which provides a 3-dimensional image.
Computed tomography (CT Scan)
Here X-rays from a finely collimated source are made to pass through a slice of the object or patient from a variety of directions. Thus X-ray beam moves all around the patient, scanning from hundreds of different angles. The computer collects the ‘slices’ of data and puts them together to form a 3-dimensional image of the body.
Ultrasonics
The human ear cannot hear sound vibrations of frequencies less than 20 Hz and greater than 2o KHz. This frequency range (20-20Khz) is audible range for human ear. Sound waves of frequencies above 20 KHz are called ultrasonic waves or ultrasonics. Though human beings cannot hear ultrasonic sound, some birds and animals are found to respond to ultrasonic sound. Bats produce and detect ultrasonic waves and are able to avoid obstacles on their way. Dogs can hear ultrasonic sound of low frequency.
Properties of ultrasonics
1. Attenuation: The amplitude of the ultrasonic waves diminishes as it propagates through a medium.
2. Ultrasonic waves undergo diffraction just like light and sound waves.
3. Ultrasonic waves require a material medium for propagation.
4. Ultrasonic waves obey law of reflection and law of refraction just like light waves.
5. Ultrasonic waves carry much more energy than audible sound waves.
6. Ultrasonic waves can penetrate large distances through matter.
7. Ultrasonic waves produce heat while passing through a medium.
Nondestructive testing using ultrasonics
Ultrasonic waves can be used to detect like cracks, cavities and the presence of foreign particles in a material. Strong pulses of ultrasonics are sent through the object to be tested. If object is defect free, then pulses will reflect from the other side. The incident pulse A and reflected pulse C are seen on the screen of CRO. If any defect is present on the object, ultrasonics gets reflected from the defect, and the reflected wave, called echo pulse B can be seen on the CRO. The position of the pulse B and its distance from A gives the nature of the defect and its location.Ultrasound scanning
Internal organs of human body can be examined via the images produced by reflection and absorption of ultrasonic waves. Here a beam of high frequency ultrasonic energy is directed into the body. Waves reflected by the body tissues are detected and transformed into an image. A computer constructs the image that reveals the shape and density of internal structures.
Through ultrasound images are much safer than x-ray images, they do not contain much defect. They also contain large amount of noises. But contain organs such as liver is impossible to scan by x-rays, but can be imaged by ultrasonic waves.
MRI Scan
80% of our body’s atoms are hydrogen atoms. Hence most parts of the body can serve as sources for hydrogen NMR signals. In MRI scan, a varying magnetic field is applied across the tissue. A radio signal can be used to flip by spies of nuclei. The signals emitted during the relaxation of protons are detected by a sensitive detector. Since the proton density varies with type of the tissue, this helps in reconstructing the image. MRI scan is better for tissues, but less effective for detecting breaks in bones. MRI scan is expensive compared to x-ray images.
Electrical method of non-destructive testing
The electrical method is based on the principle of variations in the electrical resistivity due to the presence of defect in the specimen. When a coil carrying current is held near a conductor (specimen), eddy current are induced in the conductor. This is associated with a magnetic field. The defects in the specimen will be affect the resistivity and eddy currents. As a result, induced magnetic field changes. These variations in the induced magnetic field can be detected by a search coil and hence defects can be detected.
Magnetic method of non destructive testing
In this method the specimen is magnetized by spraying a fine powder of ferromagnetic substance on the specimen. Defects produce irregularities and discontinuities in the magnetic flux lines which help to locate the size and dimension of the defects. This method can be used for magnetic materials.
FREE ELECTRON THEORY
User-agent: Mediapartners-Google
Disallow:
Classical free electron theory of metals
This theory was developed by Drude and Lorentz and hence is also known as Drude-Lorentz theory. According to this theory, a metal consists of electrons which are free to move about in the crystal like molecules of a gas in a container. Mutual repulsion between electrons is ignored and hence potential energy is taken as zero. Therefore the total energy of the electron is equal to its kinetic energy.
Drift velocity
If no electric field is applied on a conductor, the free electrons move in random directions. They collide with each other and also with the positive ions. Since the motion is completely random, average velocity in any direction is zero. If a constant electric field is established inside a conductor, the electrons experience a force F = -eE due to which they move in the direction opposite to direction of the field. These electrons undergo frequent collisions with positive ions. In each such collision, direction of motion of electrons undergoes random changes. As a result, in addition to the random motion, the electrons are subjected to a very slow directional motion. This motion is called drift and the average velocity of this motion is called drift velocity vd.
Consider a conductor subjected to an electric field E in the x-direction. The force on the electron due to the electric field = -eE.
By Newton’s law, -eE = mdvd/dt
dvd = -eEdt/m
Integrating,
Vd = -eEt/m + Constant
When t = 0, vd = 0 Therefore Constant = 0
Vd = -eEt/m --------------- (1)
Electrical conductivity
Consider a wire of length ‘dl’ and area of cross section ‘A’ subjected to an electric field E. If ‘n’ is the concentration of the electrons, the number of electrons flowing through the wire in dt seconds = nAvddt.
The quantity of charge flowing in time dt = nAvddt.e
Therefore I = dq/dt = neAvd
Current density J = I/A = nevd
Subsittuting the value of vd from (1),
J = nee Et/m = ne2Et/m --------------- (2)
By Ohm’s law, J = s E
Therefore s = J/E = ne2t/m -------------- (3)
Mobility of a charge carrier is the ratio of the drift mobility to the electric field.
µ = vd/E m2/Volt-Sec
Substituting vd from (1),
µ = et/m -------------- (4)
Substituting this in equation (3),
s = neµ ------------- (5)
Classification of semiconductors on the basis of fermi level and fermi energy
In intrinsic semiconductors, the fermilevel lie exactly at the centre of the forbidden energy gap. In n-type semiconductors fermilevel lie near the conduction band. In p-type semiconductors fermilevel lie near the valence band.
Impurity levels
In extrinsic semiconductors, addition of impurities introduces new allowed quantum energy states in the forbidden energy band. The quantum state which appears as a single energy level is known as impurity level.
Impurity level is called donor level (Ed) in n-type semiconductors and lie just below the conduction band. Impurity level is called acceptor level (Ea) in p- type semiconductor and lie just above the valence band.
Band theory of solids
The atoms in the solid are very closely packed. The nucleus of an atom is so heavy that it considered to be at rest and hence the characteristic of an atom are decided by the electrons. The electrons in an isolated atom have different and discrete amounts of energy according to their occupations in different shells and sub shells. These energy values are represented by sharp lines in an energy level diagram.
During the formation of a solid, energy levels of outer shell electrons got split up. As a result, closely packed energy levels are produced. The collection of such a large number of energy levels is called energy band. The electrons in the outermost shell are called valence electrons. The band formed by a series of energy levels containing the valence electrons is known as valence band. The next higher permitted band in a solid is the conduction band. The electrons occupying this band are known as conduction electrons.
Conduction band valence band are separated by a gap known as forbidden energy gap. No electrons can occupy energy levels in this band. When an electrons in the valence band absorbs enough energy, it jumps across the forbidden energy gap and enters the conduction band, creating a positively charged hole in the valence band.the hole is basically the deficiency of an electron.
Classification of solids on the basis of energy bands
Insulator
Insulators are very poor conductors of electricity with resitivity ranging 103 – 1017 Ωm. In this case Eg ≈ 6eV. For E.g. carbon.
Semiconductor
Conductor
Intrinsic semiconductor
A pure semiconductor free from any impurity is called intrinsic semiconductor. Here charge carriers (electrons and holes) are created by thermal excitation. Si and Ge are examples. Both Si and Ge are tetravalent. I.e. each has four valence electrons in the outermost shell. Consider the case of Ge. It has a total of 32 electrons. Out of these 32 electrons, 28 are tightly bound to the nucleus, while the remaining 4 electrons (valence electrons) revolve in the outermost orbit. In a solid, each atom shares its 4 valence electrons with its nearest neighbors to form covalent bonds.The energy needed to liberate an electron from Ge atom is very small, of the order of 0.7 eV. Thus even at room temperature, a few electrons can detach from its bonds by thermal excitation. When the electron escapes from the covalent bond, an empty space or a hole is created. The number of free electrons is always equal to the number of holes.
Extrinsic semiconductor
Extrinsic semiconductors are formed by adding suitable impurities to the intrinsic semiconductor. This process of adding impurities is called doping. Doping increases the electrical conductivity in semiconductors. The added impurity is very small, of the order of one atom per million atoms of the pure semiconductor. The added impurity may be pentavalent or trivalent. Depending on the type of impurity added, the extrinsic semiconductors can be divided into two classes: n-type and p-type.
n-type semiconductor
Disallow:
Classical free electron theory of metals
This theory was developed by Drude and Lorentz and hence is also known as Drude-Lorentz theory. According to this theory, a metal consists of electrons which are free to move about in the crystal like molecules of a gas in a container. Mutual repulsion between electrons is ignored and hence potential energy is taken as zero. Therefore the total energy of the electron is equal to its kinetic energy.
Drift velocity
If no electric field is applied on a conductor, the free electrons move in random directions. They collide with each other and also with the positive ions. Since the motion is completely random, average velocity in any direction is zero. If a constant electric field is established inside a conductor, the electrons experience a force F = -eE due to which they move in the direction opposite to direction of the field. These electrons undergo frequent collisions with positive ions. In each such collision, direction of motion of electrons undergoes random changes. As a result, in addition to the random motion, the electrons are subjected to a very slow directional motion. This motion is called drift and the average velocity of this motion is called drift velocity vd.
Consider a conductor subjected to an electric field E in the x-direction. The force on the electron due to the electric field = -eE.
By Newton’s law, -eE = mdvd/dt
dvd = -eEdt/m
Integrating,
Vd = -eEt/m + Constant
When t = 0, vd = 0 Therefore Constant = 0
Vd = -eEt/m --------------- (1)
Electrical conductivity
Consider a wire of length ‘dl’ and area of cross section ‘A’ subjected to an electric field E. If ‘n’ is the concentration of the electrons, the number of electrons flowing through the wire in dt seconds = nAvddt.The quantity of charge flowing in time dt = nAvddt.e
Therefore I = dq/dt = neAvd
Current density J = I/A = nevd
Subsittuting the value of vd from (1),
J = nee Et/m = ne2Et/m --------------- (2)
By Ohm’s law, J = s E
Therefore s = J/E = ne2t/m -------------- (3)
Mobility of a charge carrier is the ratio of the drift mobility to the electric field.
µ = vd/E m2/Volt-Sec
Substituting vd from (1),
µ = et/m -------------- (4)
Substituting this in equation (3),
s = neµ ------------- (5)
Relaxation time and mean free path
When the field E is switched off, due to the collision of the electrons with lattice ions and lattice defects, their velocity will start to decrease. This process is called relaxation. The relaxation time(t) is the time required for the drift velocity to reduce to 1/e of its initial value. The average distance traveled by an electron between two consecutive collisions is called mean free path (l) of the electron.
l = vdt -------------- (6)
Temperature dependence
The free electron theory is based on Maxwell-Boltzmann statistics.
Therefore Kinetic energy of electron = ½ mvd2 = 3/2 KBT
Vd = Ö 3KBT/m
Substituting this in equation (6),
t = lÖ m/3KBT -------------- (7)
Since s = ne2t/m, s is proportional to Ö1/T
Or r is proportional to ÖT.
Wiedmann-Franz law
The ratio of thermal conductivity to electrical conductivity of a metal is directly
proportional to absolute temperature.
K/s is proportional to T
Or, K/sT = L, a constant called Lorentz number.
L = 3KB2/2e2
Drawbacks of Classical free electron theory
1) According to this theory, r is proportional to ÖT. But experimentally it was found that r is proportional to T.
2) According to this theory, K/sT = L, a constant (Wiedmann-Franz law) for all temperatures. But this is not true at low temperatures.
3) The theoretically predicted value of specific heat of a metal does not agree with the experimentally obtained value.
4) This theory fails to explain ferromagnetism, superconductivity, photoelectric effect, Compton effect and blackbody radiation.
Quantum free electron theory
Classical free electron theory could not explain many physical properties. In 1928, Sommerfeld developed a new theory applying quantum mechanical concepts and Fermi-Dirac statistics to the free electrons in the metal. This theory is called quantum free electron theory.
Classical free electron theory permits all electrons to gain energy. But quantum free electron theory permits only a fraction of electrons to gain energy. In order to determine the actual number of electrons in a given energy range(dE), it is necessary to know the number of states(dNs) which have energy in that range. The number of states per unit energy range is called the density of states g(E).
Therefore, g(E) = dNs/dE
According to Fermi-Dirac statistics, the probability that a particular energy statewith energy E is occupied by an electron is given by,
f(E) = 1 / [1+e(E-EF/KT) ]
where EF is called Fermi level. Fermi level is the highest filled energy level at 0 K. Energy corresponding to Fermi level is known as Fermi energy. Now the actual number of electrons present in the energy range dE,
dN = f(E) g(E)dE
Effect of temperature on Fermi-Dirac distribution function
Fermi-Dirac distribution function is given by,
f(E) = 1 / [1+e(E-EF/KT) ]
At T=0K, for EEF, f(E)=0
At T=0K, for E=EF, f(E)=indeterminate
At T>0K, for E=EF, f(E)=1/2
All these results are depicted in the figure.
When the field E is switched off, due to the collision of the electrons with lattice ions and lattice defects, their velocity will start to decrease. This process is called relaxation. The relaxation time(t) is the time required for the drift velocity to reduce to 1/e of its initial value. The average distance traveled by an electron between two consecutive collisions is called mean free path (l) of the electron.
l = vdt -------------- (6)
Temperature dependence
The free electron theory is based on Maxwell-Boltzmann statistics.
Therefore Kinetic energy of electron = ½ mvd2 = 3/2 KBT
Vd = Ö 3KBT/m
Substituting this in equation (6),
t = lÖ m/3KBT -------------- (7)
Since s = ne2t/m, s is proportional to Ö1/T
Or r is proportional to ÖT.
Wiedmann-Franz law
The ratio of thermal conductivity to electrical conductivity of a metal is directly
proportional to absolute temperature.
K/s is proportional to T
Or, K/sT = L, a constant called Lorentz number.
L = 3KB2/2e2
Drawbacks of Classical free electron theory
1) According to this theory, r is proportional to ÖT. But experimentally it was found that r is proportional to T.
2) According to this theory, K/sT = L, a constant (Wiedmann-Franz law) for all temperatures. But this is not true at low temperatures.
3) The theoretically predicted value of specific heat of a metal does not agree with the experimentally obtained value.
4) This theory fails to explain ferromagnetism, superconductivity, photoelectric effect, Compton effect and blackbody radiation.
Quantum free electron theory
Classical free electron theory could not explain many physical properties. In 1928, Sommerfeld developed a new theory applying quantum mechanical concepts and Fermi-Dirac statistics to the free electrons in the metal. This theory is called quantum free electron theory.
Classical free electron theory permits all electrons to gain energy. But quantum free electron theory permits only a fraction of electrons to gain energy. In order to determine the actual number of electrons in a given energy range(dE), it is necessary to know the number of states(dNs) which have energy in that range. The number of states per unit energy range is called the density of states g(E).
Therefore, g(E) = dNs/dE
According to Fermi-Dirac statistics, the probability that a particular energy statewith energy E is occupied by an electron is given by,
f(E) = 1 / [1+e(E-EF/KT) ]
where EF is called Fermi level. Fermi level is the highest filled energy level at 0 K. Energy corresponding to Fermi level is known as Fermi energy. Now the actual number of electrons present in the energy range dE,
dN = f(E) g(E)dE
Effect of temperature on Fermi-Dirac distribution function
Fermi-Dirac distribution function is given by,
f(E) = 1 / [1+e(E-EF/KT) ]
At T=0K, for E
At T=0K, for E=EF, f(E)=indeterminate
At T>0K, for E=EF, f(E)=1/2
All these results are depicted in the figure.
Classification of semiconductors on the basis of fermi level and fermi energyIn intrinsic semiconductors, the fermilevel lie exactly at the centre of the forbidden energy gap. In n-type semiconductors fermilevel lie near the conduction band. In p-type semiconductors fermilevel lie near the valence band.
Impurity levelsIn extrinsic semiconductors, addition of impurities introduces new allowed quantum energy states in the forbidden energy band. The quantum state which appears as a single energy level is known as impurity level.
Impurity level is called donor level (Ed) in n-type semiconductors and lie just below the conduction band. Impurity level is called acceptor level (Ea) in p- type semiconductor and lie just above the valence band.
Band theory of solidsThe atoms in the solid are very closely packed. The nucleus of an atom is so heavy that it considered to be at rest and hence the characteristic of an atom are decided by the electrons. The electrons in an isolated atom have different and discrete amounts of energy according to their occupations in different shells and sub shells. These energy values are represented by sharp lines in an energy level diagram.
During the formation of a solid, energy levels of outer shell electrons got split up. As a result, closely packed energy levels are produced. The collection of such a large number of energy levels is called energy band. The electrons in the outermost shell are called valence electrons. The band formed by a series of energy levels containing the valence electrons is known as valence band. The next higher permitted band in a solid is the conduction band. The electrons occupying this band are known as conduction electrons.
Conduction band valence band are separated by a gap known as forbidden energy gap. No electrons can occupy energy levels in this band. When an electrons in the valence band absorbs enough energy, it jumps across the forbidden energy gap and enters the conduction band, creating a positively charged hole in the valence band.the hole is basically the deficiency of an electron.
Classification of solids on the basis of energy bands
Insulator
Insulators are very poor conductors of electricity with resitivity ranging 103 – 1017 Ωm. In this case Eg ≈ 6eV. For E.g. carbon.
SemiconductorA semiconductor material is one whose electrical properties lie between that of insulators and good conductors. Their forbidden band is small and resistivity ranges between 10-4to 103Ωm. Ge and Si are examples with forbidden energy gap 0.7eV and 1.1eV respectively. An appreciable number of electrons can be excited across the gap at room temperature. By adding impurities or by thermal excitation, we can increase the electrical conductivity in semiconductors
ConductorHere valence band and conduction band overlap and there is no forbidden energy gap. Resistivity ranges between 10=9 to 10-4 Ωm. Here plenty of electrons are available for electrical conduction. The electrons from valence band can freely enter the conduction band.
Intrinsic semiconductorA pure semiconductor free from any impurity is called intrinsic semiconductor. Here charge carriers (electrons and holes) are created by thermal excitation. Si and Ge are examples. Both Si and Ge are tetravalent. I.e. each has four valence electrons in the outermost shell. Consider the case of Ge. It has a total of 32 electrons. Out of these 32 electrons, 28 are tightly bound to the nucleus, while the remaining 4 electrons (valence electrons) revolve in the outermost orbit. In a solid, each atom shares its 4 valence electrons with its nearest neighbors to form covalent bonds.The energy needed to liberate an electron from Ge atom is very small, of the order of 0.7 eV. Thus even at room temperature, a few electrons can detach from its bonds by thermal excitation. When the electron escapes from the covalent bond, an empty space or a hole is created. The number of free electrons is always equal to the number of holes.
Extrinsic semiconductorExtrinsic semiconductors are formed by adding suitable impurities to the intrinsic semiconductor. This process of adding impurities is called doping. Doping increases the electrical conductivity in semiconductors. The added impurity is very small, of the order of one atom per million atoms of the pure semiconductor. The added impurity may be pentavalent or trivalent. Depending on the type of impurity added, the extrinsic semiconductors can be divided into two classes: n-type and p-type.
n-type semiconductor
When pentavalent impurity is added to pure semiconductor, it results in n-type semiconducutor. Consider the case when pentavalent Arsenic is added to pure Ge crystal. As shown in the figure, four electrons of Arsenic atom form covalent bonds with the four valence electrons of neighbouring Ge atoms. The fifth electron of Arsenic atom is not covalently bonded, but it is loosely bound to the Arsenic atom. Now by increasing the thermal energy or by applying electric field, this electron can be easily excited from the valence band to the conduction band. Thus every Arsenic atom contributes one conduction electron without creating a positive hole. Hence Arsenic is called donor element since it donates free electrons. Since current carriers are negatively charged particles, this type of semiconductor is called n-type semiconductor.
p-type semiconductor
When trivalent impurity is added to pure semiconductor, it results in p-type semiconducutor. Consider the case when trivalent Boron is added to pure Ge crystal. As shown in the figure, three valence electrons of Boron atom form covalent bonds with the three neighbouring Ge atoms. There is a deficiency of one electron (hole) in the bonding with the fourth Ge atom. The Ge atom will steal an electron from the neighbouring Ge atom to form a covalent bond. Due to this stealing action, a hole is created in the adjascent atom. This process continues. Impurity atoms that contribute hole in this manner are called acceptors. Since current carriers are positively charged particles, this type of semiconductor is called p-type semiconductor.
p-type semiconductorWhen trivalent impurity is added to pure semiconductor, it results in p-type semiconducutor. Consider the case when trivalent Boron is added to pure Ge crystal. As shown in the figure, three valence electrons of Boron atom form covalent bonds with the three neighbouring Ge atoms. There is a deficiency of one electron (hole) in the bonding with the fourth Ge atom. The Ge atom will steal an electron from the neighbouring Ge atom to form a covalent bond. Due to this stealing action, a hole is created in the adjascent atom. This process continues. Impurity atoms that contribute hole in this manner are called acceptors. Since current carriers are positively charged particles, this type of semiconductor is called p-type semiconductor.
HALL EFFECT
Hall effect
Consider a rectangular slab that carries a current I in the X-direction. A uniform magnetic field of flux density B is applied along the Z-direction. The current carriers experience a force (Lorents force) in the downward direction. This leads to an accumulation of electrons in the lower face of the slab. This makes the lower face negative. Similarly the deficiency of electrons make the upper face positive. As a result, an electric field is developed along Y-axis. This effect is called Hall effect and the emf thus developed is called Hall voltage VH. The electric field developed is called Hall field EH.
If ‘e’ is the charge of carrier and ‘v’ the velocity, then Lorentz force acting on it due to magnetic field is given by,
Fm = -e(vxB)
Since v and B are perpendicular to each other,
Fm = -evB ---------- (1)
The electric field exerts a force on charge carriers. It is given by,
Fe = EHe --------- (2)
At equilibrium,
Fm = Fe
Ie, -evB = EHe
Or EH = -Bv -------- (3)
But current density J=nev where n is the electron density.
Or v = J/ne
Substituting this in equation (3),
EH = -BJ/ne
Or EH/BJ = -1/ne = RH --------- (4)
RH is called Hall coefficient.
If the carriers are holes,
RH = 1/pe --------- (5)
Where p is the hole density.
If ‘d’, ‘w’ and ‘A’ represent the thickness, width and area of cross section of the slab respectively, then,
EH = VH/d --------- (6)
J = I/A = I/wd --------- (7)
Substituting (6) and (7) in equation (4),
RH = EH/BJ = VHw/BI
Or VH = BIRH/w = BI/wne ------------ (8)
Importance of Hall effect
Hall effect proved that band theory of solids is more accurate than free electron theory. Hall effect proved that electrons are the majority carriers in all the metals and n-type semiconductors. In p-type semiconductors, holes are the majority carriers.
Applications of Hall effect
To determine the type ( n-type or p-type) of semiconductors.
To determine the concentration of the carriers.
In nondestructive testing.
In Hall generators.
Consider a rectangular slab that carries a current I in the X-direction. A uniform magnetic field of flux density B is applied along the Z-direction. The current carriers experience a force (Lorents force) in the downward direction. This leads to an accumulation of electrons in the lower face of the slab. This makes the lower face negative. Similarly the deficiency of electrons make the upper face positive. As a result, an electric field is developed along Y-axis. This effect is called Hall effect and the emf thus developed is called Hall voltage VH. The electric field developed is called Hall field EH.If ‘e’ is the charge of carrier and ‘v’ the velocity, then Lorentz force acting on it due to magnetic field is given by,
Fm = -e(vxB)
Since v and B are perpendicular to each other,
Fm = -evB ---------- (1)
The electric field exerts a force on charge carriers. It is given by,
Fe = EHe --------- (2)
At equilibrium,
Fm = Fe
Ie, -evB = EHe
Or EH = -Bv -------- (3)
But current density J=nev where n is the electron density.
Or v = J/ne
Substituting this in equation (3),
EH = -BJ/ne
Or EH/BJ = -1/ne = RH --------- (4)
RH is called Hall coefficient.
If the carriers are holes,
RH = 1/pe --------- (5)
Where p is the hole density.
If ‘d’, ‘w’ and ‘A’ represent the thickness, width and area of cross section of the slab respectively, then,
EH = VH/d --------- (6)
J = I/A = I/wd --------- (7)
Substituting (6) and (7) in equation (4),
RH = EH/BJ = VHw/BI
Or VH = BIRH/w = BI/wne ------------ (8)
Measurement of Hall voltage and Hall coefficient
A rectangular slab of the given material having a thickness ‘d’ and width ‘w’ is placed between the pole pieces of an electromagnet with magnetic flux density B coinciding z-axis. A current I that coincides with X-axis is allowed to pass through the sample by connecting it to a battery.
The Hall voltage is measured by placing two probes at the centres of the bottom and top surfaces of the sample.
Hall coefficient RH = VHw/BI
A rectangular slab of the given material having a thickness ‘d’ and width ‘w’ is placed between the pole pieces of an electromagnet with magnetic flux density B coinciding z-axis. A current I that coincides with X-axis is allowed to pass through the sample by connecting it to a battery.
The Hall voltage is measured by placing two probes at the centres of the bottom and top surfaces of the sample.
Hall coefficient RH = VHw/BI
Importance of Hall effectHall effect proved that band theory of solids is more accurate than free electron theory. Hall effect proved that electrons are the majority carriers in all the metals and n-type semiconductors. In p-type semiconductors, holes are the majority carriers.
Applications of Hall effect
To determine the type ( n-type or p-type) of semiconductors.
To determine the concentration of the carriers.
In nondestructive testing.
In Hall generators.
SUPERCONDUCTIVITY
The electrical resistivity of many metals and alloys drops suddenly to zero when their specimens are cooled to a sufficiently low temperature, offer a temperature in the liquid helium range. This phenomenon is called superconductivity. This was first observed by Kamerlingh Onnes in 1911 while measuring the resistivity of mercury at low temperatures.
Transition temperature
The transition temperature (Tc) is the critical temperature at which the resistivity of the material suddenly changes to zero.
Transition temperature
The transition temperature (Tc) is the critical temperature at which the resistivity of the material suddenly changes to zero.
Properties of superconductorsCritical field (Hc)
When the superconducting materials are subjected to a strong magnetic field, it will result in the destruction of the superconducting property. i.e, they return to the normal state. The minimum field required to destroy the superconducting property is called the critical field (Hc). The variation of Hc with temperature is as shown.
When the superconducting materials are subjected to a strong magnetic field, it will result in the destruction of the superconducting property. i.e, they return to the normal state. The minimum field required to destroy the superconducting property is called the critical field (Hc). The variation of Hc with temperature is as shown.
Critical current density (Jc)The application of a large value of electric current to a superconducting material destroys its superconducting property. The current required for this is called critical current (Ic) and corresponding current density is called critical current density (Jc).
Specific heat
Specific heat of superconductors undergoes a discontinuous change below transition temperature.
Isotope effect
It has been observed that the superconducting transition temperature for various isotopes of a superconductor is different. This effect is known as isotope effect. This effect was discovered in isotopes of mercury by Maxwell and Reynolds in the year 1950.
Meissner effect
Meissner and Ochsenfeld in 1933 found that if a superconductor is cooled in a magnetic field below the transition temperature, the magnetic flux lines are pushed out of the body of the superconductor as shown:
This phenomenon is called Meissner effect which establishes that a superconductor is a perfect diamagnet.Therefore inside the specimen B=0
For applied fields below Hc1 the specimen is diamagnetic, exhibiting complete Meissner effect. Hc1, the flux begins to penetrate the specimen and the penetration increases until Hc2 is related. Here Meissner effect is incomplete and the specimen is said to be in a vertex (mixed) state. At Hc2, the specimen becomes a normal conductor. Hc2 is called upper critical field. They are also called hard superconductors. Eg: Nb3Sn, Nb3Ge, Nb3H etc.
BCS Theory of Superconductivity
This theory was developed by Bardeen, Cooper and Schrieffer in 1957 based on electron- lattice- electron interaction. According to this theory, an electron attracts lattice ions towards itself, so that it is surrounded by a region of positive charges. Another gets attracted to this region at high positive ion concentration. Thus an electron- lattice- electron interaction results in an electron pair formation. These pairs are called cooper pairs. They can be scattered only if the energy involved is sufficient to break it up into two single electrons.
Copper pair electrons are of opposite momenta and spin (K and –K¯). In addition, a cooper pair does not obey Pauli’s exclusion principle and hence any number of cooper pairs can be accommodated into a single quantum state.
Since an electron pair has a lower energy than the two normal electrons, there is an energy gap between the paired and the two single electrons.
As long as Cooper pair electrons remain in Cooper pair states, they do not suffer scattering and hence resistivity will be zero. When the temperature is raised, to overcome the energy gap, Cooper pair electrons gets separated to normal single electrons which may undergo scattering due to the presence of imperfections in the crystal or lattice vibrations which leads to a finite resistivity.
Josephson effect
This effect was first predicted by Josephson in 1962. The experimental arrangement was a Josephson junction which consists of a thin insulator sandwiched between two superconductors as shown:
If the insulator layer is very thin, of the order of 10-50 Å in thickness, a tunneling phenomenon called Josephson tunneling (Josephson effect) takesplace through the insulator. Thus the insulator turns into a superconductor.
I-V characteristics of a Josephson junction is as shown:
With no applied voltage, a dc current (ic) will flow across the junction. This is called dc Josephson effect. When a small voltage is applied across the junction, current oscillates with a frequency w = 4peV/h. This is called ac Josephson effect. If the applied voltage is increased beyond the critical voltage (vc), the current attains an ohmic behaviour.
Applications of superconductors
For the production of high magnetic fields.
In high energy physics experiments.
In NMR imaging.
In magnetohydrodynamic power generation.
In magnetic separation for refining ores and chemicals.
As memory storage element in computers.
In superconducting generators and motors.
In superconducting fuses, switches and cables.
In Superconducting Quantum Interference Device (SQUID).
In levitating trains.
It has been observed that the superconducting transition temperature for various isotopes of a superconductor is different. This effect is known as isotope effect. This effect was discovered in isotopes of mercury by Maxwell and Reynolds in the year 1950.
Meissner effect
Meissner and Ochsenfeld in 1933 found that if a superconductor is cooled in a magnetic field below the transition temperature, the magnetic flux lines are pushed out of the body of the superconductor as shown:
This phenomenon is called Meissner effect which establishes that a superconductor is a perfect diamagnet.Therefore inside the specimen B=0But B=H+4PM
Therefore H+4PM=0
H=-4PM
Susceptibility=M/H=-1/4P
TypeI and typeII Superconductors
In type I superconductors, magnetization curve is as shownThey are completely diamagnetic or exhibits complete Meissener effect up to critical field Hc. They are also called soft superconductors. Eg: Al, In, Sn, Pb etc.
TypeI and typeII Superconductors
In type I superconductors, magnetization curve is as shownThey are completely diamagnetic or exhibits complete Meissener effect up to critical field Hc. They are also called soft superconductors. Eg: Al, In, Sn, Pb etc.
In type II superconductors, magnetization is as shown
For applied fields below Hc1 the specimen is diamagnetic, exhibiting complete Meissner effect. Hc1, the flux begins to penetrate the specimen and the penetration increases until Hc2 is related. Here Meissner effect is incomplete and the specimen is said to be in a vertex (mixed) state. At Hc2, the specimen becomes a normal conductor. Hc2 is called upper critical field. They are also called hard superconductors. Eg: Nb3Sn, Nb3Ge, Nb3H etc.BCS Theory of Superconductivity
This theory was developed by Bardeen, Cooper and Schrieffer in 1957 based on electron- lattice- electron interaction. According to this theory, an electron attracts lattice ions towards itself, so that it is surrounded by a region of positive charges. Another gets attracted to this region at high positive ion concentration. Thus an electron- lattice- electron interaction results in an electron pair formation. These pairs are called cooper pairs. They can be scattered only if the energy involved is sufficient to break it up into two single electrons.
Copper pair electrons are of opposite momenta and spin (K and –K¯). In addition, a cooper pair does not obey Pauli’s exclusion principle and hence any number of cooper pairs can be accommodated into a single quantum state.
Since an electron pair has a lower energy than the two normal electrons, there is an energy gap between the paired and the two single electrons.
As long as Cooper pair electrons remain in Cooper pair states, they do not suffer scattering and hence resistivity will be zero. When the temperature is raised, to overcome the energy gap, Cooper pair electrons gets separated to normal single electrons which may undergo scattering due to the presence of imperfections in the crystal or lattice vibrations which leads to a finite resistivity.
Josephson effectThis effect was first predicted by Josephson in 1962. The experimental arrangement was a Josephson junction which consists of a thin insulator sandwiched between two superconductors as shown:
If the insulator layer is very thin, of the order of 10-50 Å in thickness, a tunneling phenomenon called Josephson tunneling (Josephson effect) takesplace through the insulator. Thus the insulator turns into a superconductor.I-V characteristics of a Josephson junction is as shown:
With no applied voltage, a dc current (ic) will flow across the junction. This is called dc Josephson effect. When a small voltage is applied across the junction, current oscillates with a frequency w = 4peV/h. This is called ac Josephson effect. If the applied voltage is increased beyond the critical voltage (vc), the current attains an ohmic behaviour.Applications of superconductors
For the production of high magnetic fields.
In high energy physics experiments.
In NMR imaging.
In magnetohydrodynamic power generation.
In magnetic separation for refining ores and chemicals.
As memory storage element in computers.
In superconducting generators and motors.
In superconducting fuses, switches and cables.
In Superconducting Quantum Interference Device (SQUID).
In levitating trains.
Subscribe to:
Posts (Atom)
